共识机制原理（二）—— 分布式系统

type

status

date

slug

summary

3 分布式系统一致性

重难点

系统模型

拜占庭将军问题

一致性重要定理

3.1 系统模型

一致性

分布式系统中的多个服务节点，给定一列操作，在特定协议的保障下，使这些节点对外呈现的状态是一致的，即保证集群中所有服务节点中的数据完全相同并且能够对某个提案（proposal）达成一致

系统模型的假设

每个节点的计算能力以及其失效模式

节点间通信的能力以及是否可能失效

整个系统的属性如时序等

网络模型

网络模型根据系统中的时序模式分为同步网络和异步网络

同步网络中所有节点的时钟误差存在上限，并且网络的传输时间有上限

异步网络则与同步网络相反：节点的时钟漂移无上限，消息的传输时间是任意长的，节点计算的速度也不可预料

故障模型

拜占庭 (Byzantine) 故障：这是最难处理的情况，系统内会发生任意类型的错误，发生错误的节点被称为拜占庭节点拜占庭节点不仅会出现硬件错误、宕机甚至会向其他节点发送错误消息

崩溃-恢复 (Crash-Recovery) 故障：比拜占庭类故障多了一个限制，节点总是按照程序逻辑执行，结果是正确的，但是不保证消息返回的时间

崩溃-遗漏 (Crash-Omission) 故障：比崩溃-恢复多一个非健忘的限制，即节点崩溃之前能把状态完整地保存在持久存储上，启动之后可以再次按照以前的状态继续执行和通信

崩溃-停止 (Crash-Stop) 故障：崩溃-停止是理想化的故障模型，一个节点出现故障后立即停止接收和发送所有消息，或者网络出现故障无法进行任何通信

一致性算法据此也可大致分为拜占庭容错 (Byzantine Fault Tolerance, BFT) 算法和崩溃容错 (Crash Fault Tolerance, CFT ) 算法

容错：系统的一个或多个关键部分发生故障时，能够自动地进行检测与诊断，并采取相应措施，保证设系统维持其规定功能

3.2 拜占庭将军问题

问题描述

拜占庭帝国 (Byzantine Empire) 军队的几个师驻扎在敌城外，每个师都由各自的将军指挥。将军们只能通过信使相互沟通。在观察敌情之后，他们必须制定一个共同的行动计划，如进攻 (Attack) 或者撤退 (Retreat)，且只有当半数以上的将军共同发起进攻时才能取得胜利。然而, 其中一些将军可能是叛徒，试图阻止忠诚的将军达成一致的行动计划。更糟糕的是，负责消息传递的信使也可能是叛徒，他们可能篡改或伪造消息，也可能使得消息丢失

假设

拜占庭节点的行为可以是任意的，节点之间可以共谋

节点之间的错误是不相关的且节点可以是异构的

节点之间通过异步网络连接，网络中的消息可能丢失、乱序到达、延时到达\\（拜占庭将军问题不可解）\\

节点之间传递的信息，第三方可以知晓但是不能窜改、伪造信息的内容和验证信息的完整性

内涵

在互联网生活中，其内涵可概括为：在互联网大背景下，当需要与不熟悉的对方进行价值交换活动时，人们如何才能防止不会被其中的恶意破坏者欺骗、迷惑从而作出错误的决策

在技术领域中，其内涵可概括为：在缺少可信任的中央节点和可信任的通道的情况下，分布在网络中的各个节点应如何达成共识

简介

拜占庭将军问题 (The Byzantine Generals Problem) 提供了对分布式共识问题的一种情景化描述，由 Leslie Lamport 等人在 1982 年首次发表。论文《The Byzantine Generals Problem 》同时提供了两种解决拜占庭将军问题的算法：

口信消息型解决方案 (A solution with oral message)
签名消息型解决方案 (A solution with signed message)

论文地址： Original\_Byzantine.pdf

拜占庭将军问题是分布式系统领域最复杂的容错模型，它描述了如何在存在恶意行为(如消息篡改或伪造)的情况下使分布式系统达成一致。是我们理解分布式一致性协议和算法的重要基础

达成一致的行动计划

三个将军均为忠诚的场景，经过投票表决得到结果为进攻：撤退 = 2:1，所以将一同发起进攻取得胜利

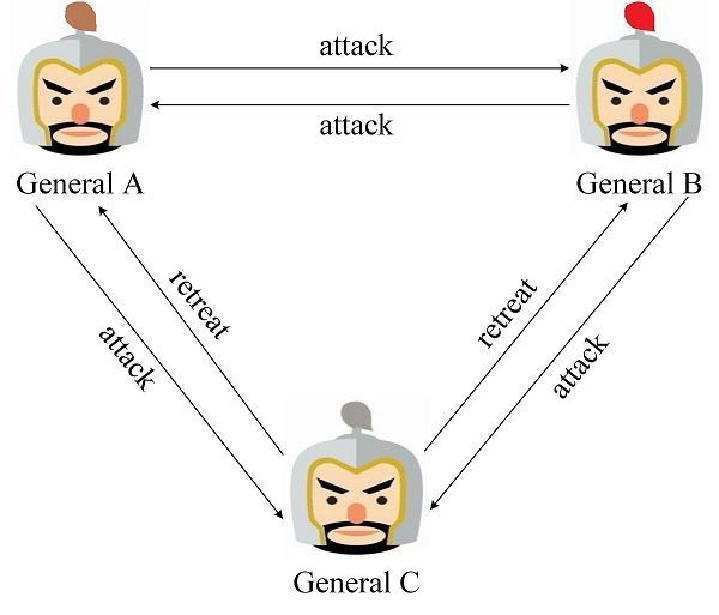
无法达成一致的行动计划

当三个将军中存在一个叛徒时，将可能扰乱正常的作战计划。论文中给出了一个更加普适的结论：如果存在 m 个叛将，那么至少需要 3m+1 个将军，才能最终达到一致的行动方案

口信消息型解决方案 (A solution with oral message)

对于口信消息 (Oral message) 的定义如下：

A1. 任何已经发送的消息都将被正确传达

A2. 消息的接收者知道是谁发送了消息

A3. 消息的缺席可以被检测

在口信消息型解决方案中，首先发送消息的将军称为指挥官，其余将军称为副官。对于 3 忠 1 叛的场景需要进行两轮作战信息协商，如果没有收到作战信息那么默认撤退

如上所述，对于口信消息型拜占庭将军问题，如果叛将人数为 m，将军人数不少于 3m+1，那么最终能达成一致的行动计划。值的注意的是，在这个算法中，叛将人数 m 是已知的，且叛将人数 m 决定了递归的次数，即叛将数 m 决定了进行作战信息协商的轮数，如果存在 m 个叛将，则需要进行 m+1 轮作战信息协商。这也是上述存在 1 个叛将时需要进行两轮作战信息协商的原因

签名消息型解决方案 (A solution with signed message)

对签名消息的定义是在口信消息定义的基础上增加了如下两条：

A4. 忠诚将军的签名无法伪造，而且对他签名消息的内容进行任何更改都会被发现

A5. 任何人都能验证将军签名的真伪

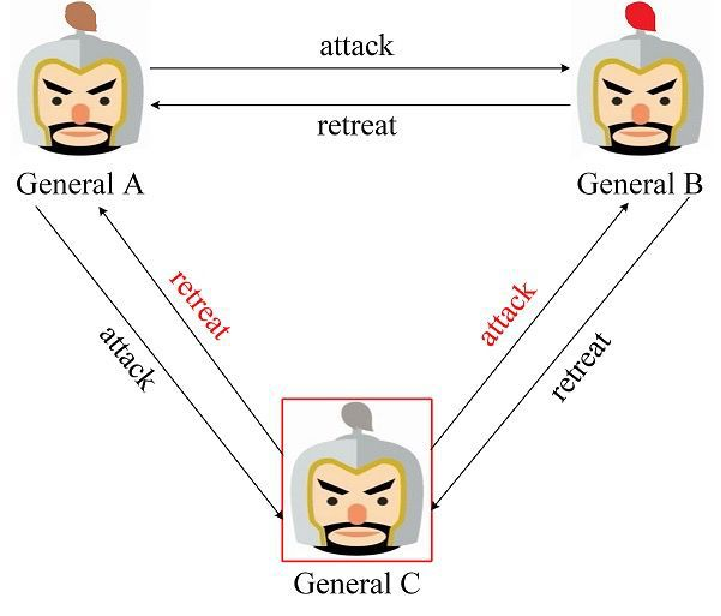
忠将率先发起作战协商的场景，General A 率先向 General B、C 发送了进攻消息，一旦叛将 General C 篡改了来自 General A 的消息，那么 General B 将发现作战信息被 General C 篡改，General B 将执行 General A 发送的消息

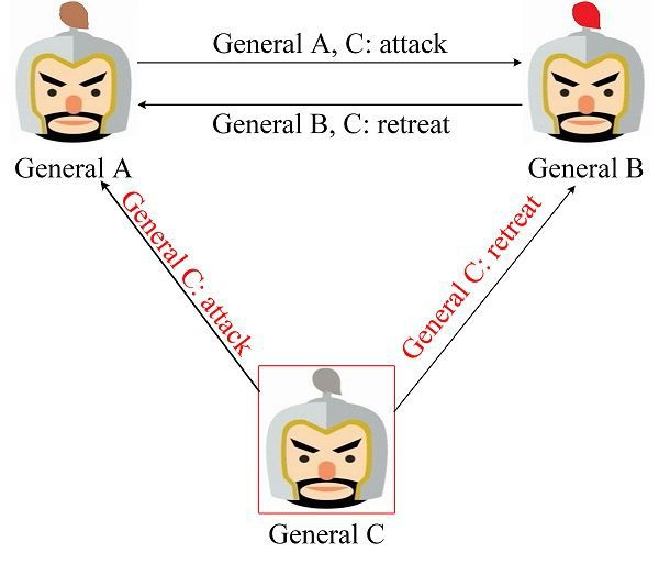
叛将率先发起作战协商的场景，叛将 General C 率先发送了误导的作战信息，那么 General A、B 将发现 General C 发送的作战信息不一致，因此判定其为叛将。可对其进行处理后再进行作战信息协商

3.3 一致性重要定理

FLP 定理

FLP Impossibility（FLP不可能性）是分布式领域中一个非常著名的结果

该定理的论文是由 Fischer， Lynch and Patterson 三位作者于 1985 年发表，之后该论文毫无疑问得获得了 Dijkstra 奖

FLP 给出了一个的结论：在异步通信场景，即使只有一个进程失败，也没有任何算法能保证非失败进程达到一致性

非失败进程指的是成功或无响应状态的进程

FLP 定理 — 模型

异步通信

与同步通信的最大区别是没有时钟、不能时间同步、不能使用超时、不能探测失败、消息可任意延迟、消息可乱序

通信健壮

只要进程非失败，消息虽会被无限延迟，但最终会被送达；并且消息仅会被送达一次（无重复）

fail-stop 模型

进程失败如同宕机，不再处理任何消息。相对 Byzantine 模型，不会产生错误消息

失败进程数量

最多一个进程失败

分布式算法衡量的标准

我们在衡量一个分布式算法是否正确时有三个标准：

Termination（终止性）：非失败进程最终可以做出选择

Agreement（一致性）：所有的进程必须做出相同的决议

Validity（合法性）：进程的决议值，必须是其他进程提交的请求值

终止性描述了算法必须在有限时间内结束，不能无限循环下去；一致性描述了我们期望的相同决议；合法性是为了排除进程初始值对自身的干扰

案例分析

假如我们设计一个算法 P，每个节点根据多数派表决的方式判断本地是提交还是回滚：

假如 C 收到了 A、B 的提交申请，收到了 D 的回滚申请，而 C 本身也倾向于回滚，此时，提交、回滚各有两票，E 的投票决定着 C 的最终决议。而此时，E 失败了，或者 E 发送给 C 的消息被无限延迟（无法探测失败），此时 C 选择一直等待，或者按照某种既定的规则选择提交或失败，后续可能 E 正常而 C 失败，总之，导致 C 没有做出最终决策，或者 C 做了最终决策失败后无人可知。称所有进程组成的状态为 Configuration，如果一系列操作之后，没有进程做出决策称为“不确定的”Configuration；不确定 Configuration 的意思是，后续可能做出提交，也可能做出回滚的决议

相反，如果某个 Configuration 能准确地说会做出提交/回滚的决议，则称为“确定性”的 Configuration。如果某个 Configuration 是确定的，则认为一致性是可以达成

对上述算法 P，可能存在一种极端场景，每次都构造出一个“不确定”的 Configuration，比如每次都是已经做出决议的 C 失败，而之前失败的 E 复活（在异步场景中，无法真正区分进程是失败，还是消息延迟），也就是说，因为消息被延迟乱序，导致结果难以预料

而 FLP 证明也是遵循这个思路，在任何算法之上，都能构造出这样一些永远都不确定的 Configuration，也就没有任何理论上的具体的算法，能避免这种最坏情况

CAP 理论

CAP 理论是由 Eric Brewer 提出的分布式系统中最为重要的理论之一。CAP 理论的定义很简单，CAP 三个字母分别代表了分布式系统中三个相互矛盾的属性：

Consistency (一致性) ：CAP 理论中的副本一致性特指强一致性

Availability(可用性) ：指系统在出现异常时已经可以提供服务

Tolerance to the partition of network (分区容忍) ：指系统可以对网络分区这种异常情况进行容错处理

CAP 理论指出：无法设计一种分布式协议，使得同时完全具备 CAP 三个属性，即 1) 该种协议下的副本始终是强一致性，2) 服务始终是可用的，3) 协议可以容忍任何网络分区异常

分布式系统协议只能在 CAP 这三者间有所折中

基于 CAP 定理，需要根据不同场景的不同业务要求来进行算法上的权衡。对于分布式存储系统来说，网络连接故障是无法避免的，在设计系统时不得不考虑分区容忍性，实际上只能在一致性和可用性之间进行权衡

CAP 理论的详细证明可以参考相关论文。这里可以简单用一个反例证明不存在 CAP 兼具的系统。假设系统只有两个副本 A 和 B，Client 更新这两个副本，假设在网络分化时，Client 与副本 A 可以正常通信，但副本 B 与 Client、副本 B 与副本 A 无法通信，此时，Client 对副本 A 更新的信息永远无法同步到副本 B 上。如果希望系统依旧具有强一致的属性，则此时需要停止更新服务，即不再修改数据，从而让副本 A 与副本 B 保持一致；如果希望系统依旧可以提供更新服务，则只能更新副本 A 而无法更新副本 B，此时无法保证副本 A 与副本 B 一致

CAP 定理表明虽然不能使某个分布式场景同时满足三个性质，但可以使之同时满足三个中的两个。更进一步说，对于包含多个分布式场景的分布式系统，可以在满足三个性质的程度上进行适当的权衡。基于 CAP 定理，需要根据不同场景的不同业务要求来进行算法上的权衡。对于分布式存储系统来说，网络连接故障是无法避免的，在设计系统时不得不考虑分区容忍性，实际上只能在一致性和可用性之间进行权衡。用一致性模型来描述一致性强弱分为强一致性模型和弱一致性模型，其中弱一致性模型主要考虑最终一致性，最终一致性是系统保证最终所有的访问将返回这个对象的最后更新值